Επόμενο:10.3 Υλοποίηση των Δεξαμενών Εργασίας Πάνω: Κεφάλαιο 10o : Αντίγραφα Εργαζομένων Πίσω: 10.1 Δεξαμενές Εργασίας

10.2 Αλγόριθμος Συντομότερου Μονοπατιού

Για να γίνει κατανοητό το υπόδειγμα παράλληλου προγραμματισμού των Αντιγράφων Εργαζομένων χρησιμοποιούμε τον αλγόριθμο του Συντομότερου Μονοπατιού για την εύρεση του συντομότερου μονοπατιού μεταξύ δύο κόμβων ενός γραφήματος. Ειδικότερα, θα θεωρήσουμε ένα πρόβλημα συντομότερου μονοπατιού στο οποίο υπάρχει μια μόνο αφετηρία και θέλουμε να βρούμε τη συντομότερη απόσταση ανάμεσα σε έναν δεδομένο κόμβο αφετηρίας και έναν οποιονδήποτε άλλο κόμβο του γραφήματος. Καταρχήν θα περιγράψουμε έναν ακολουθιακό αλγόριθμο συντομότερου μονοπατιού και στην συνέχεια μια απλή παράλληλη έκδοση χρησιμοποιώντας μια Δεξαμενή Εργασίας. Στις επόμενες παραγράφους θα περιγράψουμε την εφαρμογή της Δεξαμενής Εργασίας σε συστήματα διαμοιραζόμενης μνήμης.

Τα γραφήματα είναι χρήσιμα μαθηματικά εργαλεία για τη μοντελοποίηση διαφόρων διαδικασιών. Χρησιμοποιούνται σε πολλούς τομείς της μηχανικής, των φυσικών επιστημών και των κοινωνικών επιστημών. Ουσιαστικά ένα γράφημα είναι ένα πολύ απλό αντικείμενο: ένα πεπερασμένο σύνολο κόμβων και ένα πεπερασμένο σύνολο ακμών που συνδέει αυτούς τους κόμβους. Σε ένα προσανατολισμένο γράφημα κάθε ακμή έχει έναν προσανατολισμό που προσδιορίζει από ποιόν κόμβο ξεκινάει και που καταλήγει. Σε ένα γράφημα με βάρη κάθε ακμή έχει ένα βάρος, που είναι ένας αριθμός. Το σχήμα 10. 2 δείχνει ένα παράδειγμα προσανατολισμένου γραφήματος με βάρος με πέντε κόμβους (A, B, C, D, E) και επτά ακμές κάθε μία με ένα βάρος που είναι ένας θετικός ακέραιος.

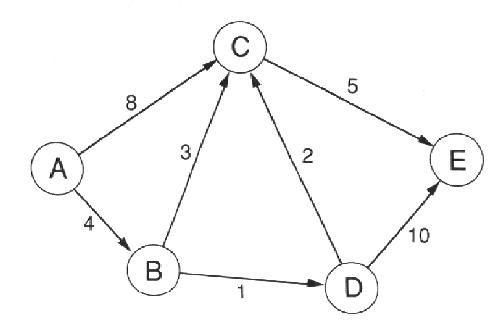
ΣΧΗΜΑ 10.2 Κατευθυνόμενο γράφημα με βάρη

Ένα γράφημα μπορεί να χρησιμοποιηθεί για να αναπαραστήσει αεροπορικά κόστη μεταξύ πόλεων, όπου κάθε κόμβος είναι μια πόλη και κάθε βάρος είναι το κόστος ταξιδιού μεταξύ δύο πόλεων. Εναλλακτικά, τα βάρη μπορεί να παριστάνουν αποστάσεις μεταξύ πόλεων ή διάρκεια ταξιδιού μεταξύ πόλεων. Ένα γράφημα μπορεί επίσης να αναπαριστάνει εναλλακτικές μεθόδους για την επίτευξη ενός σκοπού, όπου κάθε ακμή είναι κάποια εργασία που πρέπει να πραγματοποιηθεί και το αντίστοιχο βάρος της απαιτήσεις σε εργατικό δυναμικό για την πραγματοποίηση αυτής της εργασίας. Σε όλα αυτά τα παραδείγματα εφαρμογών είναι χρήσιμο να γνωρίζουμε το συντομότερο μονοπάτι από έναν δεδομένο κόμβο-αφετηρία σε άλλους κόμβους προορισμούς. Στην περίπτωση του κόστους αεροπορικών εισιτηρίων, το συντομότερο μονοπάτι στο γράφημα θα είναι το ελάχιστο εισιτήριο για το ταξίδι ανάμεσα σε δυο πόλεις. Στην περίπτωση του γραφήματος εργασιών-εργατικού δυναμικού το συντομότερο μονοπάτι θα δηλώνει την κατάλληλη σειρά εργασιών που πρέπει να πραγματοποιηθούν για να επιτευχθεί ένας στόχος με το ελάχιστο δυνατό εργατικό δυναμικό.

10.2.1 Ακολουθιακός Αλγόριθμος Συντομότερου Μονοπατιού

Για να διαμορφώσουμε τον αλγόριθμο του συντομότερου μονοπατιού χρειάζεται πρώτα μια δομή δεδομένων για να αναπαραστήσουμε το προσανατολισμένο γράφημα. Οι κόμβοι του γραφήματος μπορούν να αριθμηθούν από το 0 ως το n και τα βάρη να αναπαρασταθούν με τον δι-διάστατο πίνακα weight, στον οποίο το βάρος το βάρος μιας ακμής από τον κόμβο i στον j αποθηκεύεται στη θέση weight[i,j]. Αν δεν υπάρχει ακμή από τον κόμβο i στον j τότε το weight[i,j] είναι άπειρο. Ο αριθμός των ακμών n και ο δι-διάστατος πίνακας weight αρκούν για την αναπαράσταση οποιουδήποτε προσανατολισμένου γραφήματος με βάρος. Παρακάτω δίνουμε τον πίνακα weight του γραφήματος του σχήματος 10.2:

                                        inf              4                8              inf              inf

                                        inf              inf              3              1                inf

                                        inf              inf              inf              inf              5

                                        inf              inf              2              inf              10

                                        inf              inf              inf              inf              inf

Αρίθμηση κόμβων:

A=1;     B=2;     C=3;      D=4;     E=5;

Ο πίνακας weight έχει μια πεπερασμένη τιμή για κάθε ακμή του γραφήματος. Χρειάζονται δύο επιπλέον δομές δεδομένων για να εκφράσουμε τον αλγόριθμο του συντομότερου μονοπατιού. Ο αλγόριθμος θα υπολογίζει την πιο κοντινή απόσταση από έναν κόμβο αφετηρία (θα υποθέτουμε πάντα πως είναι ο κόμβος 1) προς έναν οποιοδήποτε άλλο κόμβο του γραφήματος. Ο πίνακας mindist χρησιμοποιείται για να καταγράφει την συντομότερη απόσταση προς κάθε κόμβο. Καθώς ο αλγόριθμος προχωρεί ο mindist αποθηκεύει την συντομότερη απόσταση που έχει βρει μέχρι εκείνη τη στιγμή προς κάθε κόμβο. Τα στοιχεία αυτού του πίνακα συνεχώς αλλάζουν τιμές μέχρι ο αλγόριθμος να τελικά να τερματίσει με τις σωστές απαντήσεις. Επίσης, χρειάζεται μια ουρά για να κρατάει τους αριθμούς των κόμβων. Οι κόμβοι συνεχώς αφαιρούνται και προστίθενται σε αυτή την ουρά κατά τη διάρκεια της εκτέλεσης του αλγορίθμου.

Για να γίνει περισσότερο κατανοητός ο αλγόριθμος του συντομότερου μονοπατιού θεωρείστε ένα συγκεκριμένο στιγμιότυπο κατά τη διάρκεια της εκτέλεσης του στο οποίο ο mindist καταγράφει τη συντομότερη απόσταση που βρέθηκε μέχρι τότε προς κάθε κόμβο. Τώρα έστω ότι βρέθηκε μια νέα συντομότερη απόσταση προς τον κόμβο x και αποθηκεύθηκε στο mindist[x]. Θεωρείστε κάποια ακμή που εξέρχεται από τον κόμβο x προς τον κόμβο w με βάρος το weight[x,w]. Το μονοπάτι προς τον κόμβο x μπορεί τώρα να επεκταθεί ως τον κόμβο w με την ακμή αυτή και το μονοπάτι αυτό θα έχει απόσταση: newdist:= mindist[x]+weight[x,w]. Στην συνέχεια το newdist συγκρίνεται με την τρέχουσα τιμή του mindist[w]. Αν είναι μικρότερο τότε βρέθηκε μια πιο σύντομη διαδρομή προς τον κόμβο w και το mindist[w] ενημερώνει την τιμή του με αυτή τη νέα τιμή newdist. Επίσης πρέπει να ελεγχθούν και οι ακμές που εξέρχονται από τον κόμβο w. Πρώτα όμως πρέπει να εξεταστούν οι ακμές που έχουν μείνει και που εξέρχονται από τον κόμβο x, έτσι ώστε ο κόμβος w να εισαχθεί στην ουρά των κόμβων.

Κάθε φορά που βρίσκεται μια πιο σύντομη απόσταση προς οποιονδήποτε κόμβο του γραφήματος τότε ο κόμβος τοποθετείται στην ουρά. Οι κόμβοι αφαιρούνται ένας κάθε φορά από τη ουρά και όλες οι ακμές που εξέρχονται εξετάζονται. Αυτό μπορεί να οδηγήσει στην πρόσθεση νέων κόμβων στην ουρά. Σταδιακά, καθώς βρίσκονται όλα τα σύντομα μονοπάτια το μέγεθος της ουράς μικραίνει. Όταν η ουρά είναι άδεια ο αλγόριθμος τερματίζεται. Παρακάτω δίνουμε μια πιο ακριβή περιγραφή αυτού του ακολουθιακού Αλγόριθμου Συντομότερου Μονοπατιού:

Initialize mindist array to infinity;


Initialize queue to contain source vertex 1;


mindist[1]:= 0;


While queue is not empty do


Begin


    x:= head of queue;


    For w:= 1 to n do


    Begin


        newdist:= mindist[x]+weight[x,w];    


        If newdist < mindist[w] then

        Begin

            mindist[w]:= newdist;

            If w not in queue then append w to queue

        End;

    End;

End;

10.2.2 Παράλληλος Αλγόριθμος Συντομότερου Μονοπατιού

Στον ακολουθιακό αλγόριθμο η ουρά χρησιμοποιείται για να διατηρεί τους κόμβους έτσι ώστε να τους επεξεργαστούμε αργότερα. Όμως, δεν υπάρχει κανένας λόγος να επεξεργαστούμε αυτές τις εισαγωγές των κόμβων με κάποια συγκεκριμένη ακολουθία. Στην πραγματικότητα δεν υπάρχει κανένας λόγος που να μην επιτρέπει την επεξεργασία όλων των κόμβων του πίνακα παράλληλα. Αυτή η παρατήρηση είναι το κλειδί που δημιουργεί την παράλληλη έκδοση του αλγορίθμου του συντομότερου μονοπατιού. Η ουρά των κόμβων μπορεί να μετατραπεί σε Δεξαμενή Εργασίας των αριθμών των κόμβων. Ένα σύνολο παράλληλων διεργασιών εργαζομένων μπορεί να αφαιρεί κόμβους από την Δεξαμενή Εργασίας, να τους επεξεργάζεται και να προσθέτει νέους κόμβους στη Δεξαμενή. Όταν η Δεξαμενή Εργασίας αδειάσει τότε ο αλγόριθμος τερματίζεται.

Ο κώδικας για κάθε εργαζόμενο της παράλληλης έκδοσης είναι σχεδόν ο ίδιος με το ακολουθιακό πρόγραμμα που είδαμε παραπάνω. Αυτή η ενέργεια της ακολουθιακής εξέτασης των κόμβων επαναλαμβάνεται στους εργαζόμενους, με κάθε εργαζόμενο να εκτελεί στην ουσία τον ίδιο κώδικα. Η διαδικασία για τους εργαζόμενους φαίνεται στο σχήμα 10.3. Σε κάθε εργαζόμενο δίνεται ένας μοναδικός αναγνωριστικός αριθμός, ο me, που περνιέται στις ρουτίνες Getwork και Putwork ως επιπλέον παράμετρος. Στις επόμενες παραγράφους του κεφαλαίου που ασχολούνται με το θέμα της εφαρμογής των Getwork και Putwork θα δούμε ότι αυτοί οι αναγνωριστικοί αριθμοί διεργασιών είναι χρήσιμοι στην εξισορρόπηση φορτίου της Δεξαμενής Εργασίας.

PROGRAM Shortpath;


CONST n=…; (*Αριθμός των κόμβων*)


    numworkers=…; (*Αριθμός των διεργασιών Εργαζομένων*)


    infinity=32000;


TYPE worktype= INTEGER; (*Κάθε στοιχείο στη Δεξαμενή Εργασίας είναι ένας αριθμός κόμβου*)


VAR weight: ARRAY [1..n,1..n] OF INTEGER;


    i,j: INTEGER;


    mindist: ARRAY [1..n] OF INTEGER; (*Ελάχιστη απόσταση προς κάθε κόμβο*)


    L: ARRAY [1..n] OF SPINLOCK;


    inflag: ARRAY [1..n] OF BOOLEAN; (*Αληθής αν ο κόμβος βρίσκεται στην Δεξαμενή Εργασίας*)


    startvertex: worktype;

 


PROCEDURE Getwork(me: INTEGER; VAR item: worktype);


… (*Δέχεται ενα περιγραφέα εργασίας στο “item”*)

 


PROCEDURE Putwork(me: INTEGER; item: worktype);


… (*Πρόσθεση του “item” στη Δεξαμενή Εργασίας*)

 


PROCEDURE Worker(me: INTEGER);


VAR vertex: worktype;


    w,newdist: INTEGER;


BEGIN


    Getwork(me, vetrex); (*Λαμβάνω έναν νέο αριθμό κόμβου για εξέταση*)


    WHILE vertex < > -1 DO

    BEGIN

        inflag[vertex]:= FALSE; (*Ο κόμβος αφαιρείται από τη Δεξαμενή Εργασίας*)

        FOR w:= 1 TO n DO (*Επεξεργασία όλων των εξερχόμενων ακμών του “vertex”*)

        BEGIN

            IF weight[vertex] < infinity THEN

            BEGIN (*Ελέγχουμε αν αυτό είναι ένα συντομότερο μονοπάτι προς τον w*)

                newdist:= mindist[vertex]+weight[vertex,w];

                Lock(L[w]); (*Αμοιβαίος αποκλεισμός στο “mindist[w]”*)

                IF newdist < mindist THEN (*Κλείδωμα*)

                BEGIN

                    mindist[w]:= newdist; (*Ενημέρωση της απόστασης σε “w”*)

                    Unlock(L[w]);

                    IF not inflag[w] THEN (*Αν το “w” δεν υπάρχει στη Δεξαμενή Εργασίας*)

                    BEGIN

                        inflag[w]:= TRUE;

                        Putwork(me,w}; (*Τοποθέτηση του “w” στη Δεξαμενή*)

                    END;

                END

                ELSE Unlock(L[w]); (*Ξεκλέιδωμα*)

        END;

    END;

    Getwork(me,vertex); (*Παίρνω νέο αριθμό κόμβου*)

END;

END;

 

BEGIN (*Κυρίως πρόγραμμα*)

 

… (*Ανάγνωση των τιμών για τον πίνακα weight*)

 

    FOR i:= 1 TO n DO (*Αρχικοποίηση των mindist και inflag*)

    BEGIN

        mindist[i]:= infinity;

        inflag[i]:= FALSE;

    END;

    mindist[startvertex]:= 0;

    inflag[startvertex]:= TRUE;

    FORALL i:= 1 TO numworkers DO (*Δημιουργία των Αντιγράφων Εργαζομένων*)

        Worker(i);

 

… (*Τελικές απαντήσεις που βρίσκονται στον πίνακα “mindist”*)

 

END.

ΣΧΗΜΑ 10.3 Παράλληλος Αλγόριθμος Συντομότερου Μονοπατιού

Κάθε Εργαζόμενος αρχίζει με μια κλήση Getwork(me,vertex) η οποία δέχεται τον αριθμό κόμβου από τη Δεξαμενή Εργασίας στην τοπική μεταβλητή vertex. Όταν η Δεξαμενή Εργασίας είναι άδεια και όλοι οι Εργαζόμενοι περιμένουν σε αυτή την άδεια Δεξαμενή, τότε η ρουτίνα Getwork θα επιστρέψει το σήμα τερματισμού (-1) σε όλους τους Εργαζόμενους. Κάθε Εργαζόμενος έχει έναν βρόχο WHILE που συνεχίζει την επεξεργασία των κόμβων από τη Δεξαμενή Εργασίας μέχρι να λάβει το σήμα τερματισμού. Η διαδικασία Worker είναι στη ουσία η ίδια με τον ακολουθιακό αλγόριθμο συντομότερου μονοπατιού που είδαμε προηγουμένως. Η μόνη διαφορά είναι ότι όταν ανακαλύπτεται μια νέα συντομότερη διαδρομή προς τον κόμβο w, ο αριθμός του κόμβου τοποθετείται στη Δεξαμενή Εργασίας, χρησιμοποιώντας την Putwork(me,w), και όχι στην ουρά όπως στην ακολουθιακή έκδοση.

Στην καρδιά της διαδικασίας Worker υπάρχει μια λειτουργία ελέγχου και τροποποίησης στην mindist[w]. Εφόσον αυτή η λειτουργία πραγματοποιείται από όλους τους παράλληλους Εργαζόμενους απαιτεί να υπάρχει αμοιβαίος αποκλεισμός στη mindist[w]. Αυτό εξασφαλίζεται με την ενεργοποίηση και την απενεργοποίηση του κλειδώματος L[w]. Μια ενδιαφέρουσα πτυχή της διαδικασίας Worker είναι η χρήση του πίνακα inflag που δηλώνει αν κάθε κόμβος βρίσκεται ή όχι στη Δεξαμενή Εργασίας. Εφόσον υπάρχει λειτουργία ελέγχου και τροποποίησης στην inflag[w], μπορεί να χρησιμοποιηθεί ο αμοιβαίος αποκλεισμός για να την κάνει μια ατομική λειτουργία. Από τη στιγμή που δεν είναι ατομική λειτουργία είναι δυνατόν να μπουν δύο αντίγραφα του ίδιου αριθμού κόμβου να μπουν στη Δεξαμενή Εργασίας. Όμως, αυτό το απίθανο γεγονός έχει ως αποτέλεσμα μόνο επιπλέον υπολογισμούς και δεν προκαλεί κανένα λάθος. Συνεπώς, η επιπλέον επιβάρυνση του αμοιβαίου αποκλεισμού δεν δικαιολογείται σε αυτή την περίπτωση.

Αν το συγκεκριμένο γράφημα είναι πυκνό, με κάθε κόμβο να είναι απευθείας συνδεδεμένος στους περισσότερους κόμβους, τότε ο δι-διάστατος πίνακας weight είναι η κατάλληλη δομή δεδομένων για την αναπαράσταση του γραφήματος. Όμως, αν το γράφημα είναι αραιό, με κάθε κόμβο να έχει έναν σχετικά μικρό αριθμό εξερχόμενων ακμών, μπορεί να χρησιμοποιηθεί μια πιο αποδοτική δομή δεδομένων: μια λίστα ακμών για κάθε κόμβο. Η διαδικασία Worker μπορεί στην περίπτωση αυτή να τροποποιηθεί και να επαναλαμβάνεται στη λίστα ακμών για το δεδομένο κόμβο. Αυτή η μικρή τροποποίηση της διαδικασίας Worker αφορά μια από τις ασκήσεις στο τέλος του κεφαλαίου.

Επόμενο:10.3 Υλοποίηση των Δεξαμενών Εργασίας Πάνω: Κεφάλαιο 10o : Αντίγραφα Εργαζομένων Πίσω: 10.1 Δεξαμενές Εργασίας