6.1 Επιλύνοντας μια Διαφορική Εξίσωση

Επόμενο:6.2. Παράλληλος Αλγόριθμος Jacobi Πάνω: Κεφάλαιο 6o : Σύγχρονος παραλληλισμός Πίσω: Κεφάλαιο 6o : Σύγχρονος παραλληλισμός

6.1 Επιλύνοντας μια Διαφορική Εξίσωση

Οι περισσότερες υπολογιστικές αριθμητικές τεχνικές χρησιμοποιούν τεράστιους πίνακες πολλών διαστάσεων ως πρωτεύουσα δομή δεδομένων. Η επεξεργασία των στοιχείων αυτών των πινάκων μπορεί να οδηγήσει σε παράλληλες εκδόσεις των δημοφιλών αριθμητικών αλγορίθμων. Ένας τέτοιος αριθμητικός αλγόριθμος υπολογισμών είναι ο αλγόριθμος Jacobi που επιλύει ένα σημαντικό τύπο διαφορικών εξισώσεων που ονομάζεται εξίσωση του Laplace. Σαν ένα παράδειγμα εφαρμογής αυτού του αλγορίθμου θεωρούμε ένα αγώγιμο φύλλο υλικού δύο διαστάσεων στο οποίο εφαρμόζουμε τάση και στις τέσσερις άκρες του. Η τάση διαφέρει κατά μήκος των άκρων, αλλά διατηρείται σταθερή σε κάθε άκρο. Για να καθορίσουμε ένα τελικό πρότυπο τάσεων για όλα τα εσωτερικά σημεία του φύλλου πρέπει να επιλυθεί η εξίσωση του Laplace για όλα τα εσωτερικά σημεία.

Έστω ότι το v(x,y) αναπαριστά την επιθυμητή συνάρτηση που αναφέρει την τάση κάθε σημείου (x,y) στο φύλλο μετάλου. Τότε η εξίσωση του Laplace έχει τη μορφή :

Η εξίσωση του Laplace είναι μια γραμμική μερική διαφορική εξίσωση και αποτελεί μια σημαντική κατηγορία εξισώσεων που εμφανίζεται ιδιαίτερα συχνά. Αυτή η εξίσωση μπορεί να λυθεί αριθμητικά αν θεωρήσουμε ένα διδιάστατο πλέγμα σημείων στην επιφάνεια του αγώγιμου φύλλου. Αυτό το αγώγιμο φύλλο φαίνεται στο σχήμα 6.1. Για να λάβουμε μια ακριβέστερη λύση της εξίσωσης ο αριθμός των σημείων του πλέγματος μπορεί να αυξηθεί, αλλά θα αυξηθεί επίσης και ο αριθμός των υπολογισμών που απαιτούνται. Εφαρμόζοντας την εξίσωση του Laplace στο πλέγμα σημείων, η εξίσωση από διαφορική μετατρέπεται σε εξίσωση διαφορών, που μπορεί να λυθεί αριθμητικά σε έναν υπολογιστή.

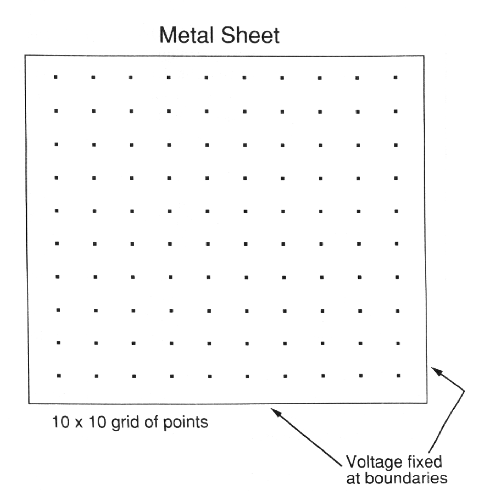
ΣΧΗΜΑ 6.1 Δίκτυο σημείων για την εξίσωση του Laplace

Έστω ότι η τάση ενός σημείου του πλέγματος (i,j) είναι V(i,j). Εφαρμόζοντας την εξίσωση του Laplace στα αποτελέσματα πλέγματος έχουμε την ακόλουθη εξίσωση διαφορών, που σχετίζει την τάση στα γειτονικά σημεία του πλέγματος :

Η παραπάνω εξίσωση διαφορών δηλώνει μια απλή σχέση μεταξύ των τάσεων των γειτονικών σημείων: η τάση κάθε σημείου είναι ο μέσος όρος της τάσης των τεσσάρων γειτονικών σημείων. Η σχέση αυτή φαίνεται στο σχήμα 6.2. Η εξίσωση διαφορών παρέχει μια απλή υπολογιστική τεχνική επίλυσης της εξίσωσης. Το πρώτο βήμα είναι η επιλογή κάποιων αρχικών τιμών τάσεων κάθε σημείου του πλέγματος. Εφόσον η τάση όλων των γειτονικών σημείων διατηρείται σταθερή οι τάσεις που ζητάμε στο πρώτο βήμα είναι ήδη γνωστές. Η αρχική τιμή όλων των εσωτερικών σημείων μπορεί αρχικά να τεθεί αυθαίρετα ίση με το μηδέν. Στη συνέχεια η επανάληψη που ακολουθεί επαναλαμβάνεται αρκετές φορές σε αυτές τις τιμές: η τιμή κάθε σημείου του πλέγματος υπολογίζεται ξανά από το μέσο όρο των τεσσάρων γειτονικών σημείων. Αυτή η υπολογιστική μεθοδολογία ονομάζεται Χαλάρωση Jacobi. Το σχήμα 6.2 απεικονίζει τη γενική ιδέα πίσω από αυτή τη μέθοδο.

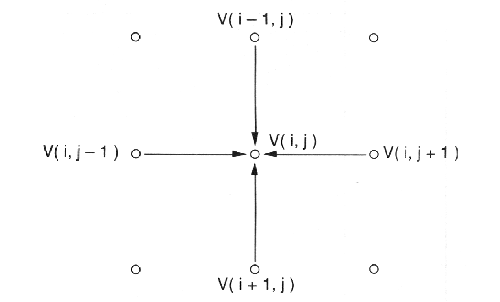
ΣΧΗΜΑ 6.2 Υπολογισμός της τάσης κάθε σημείου

Είναι φανερό ότι αν θέλουμε όλες οι τιμές των σημείων του πλέγματος να είναι ίσες με το μέσο όρο των γειτονικών τους, τότε αντικαθιστώντας επαναληπτικά κάθε τιμή με το μέσο όρο των γειτονικών της θα επιτύχουμε τελικώς αυτό το στόχο. Εφόσον τα οριακά σημεία διατηρούν την κατάλληλη προκαθορισμένη τους τιμή, θα ενεργήσουν σαν αναφορά στην προσπάθεια καθορισμού των τιμών όλων των εσωτερικών σημείων, τα οποία αλλάζουν σε κάθε επανάληψη. Αυτή η επαναληπτική μέθοδος έχει αναλυθεί μαθηματικά και έχει προκύψει ότι σταδιακά συνεχώς προσεγγίζει, με κάθε διαδοχική επανάληψη, μια πιο ακριβή λύση. Για επιπλέον λεπτομέρειες πάνω σε αυτή αλλά και σε άλλες επαναληπτικές μεθόδους υπάρχει αναφορά στους Bertsekas and Tsitsiklis [1989] και Hageman and Young [1981].

Ο αλγόριθμος Jacobi για την επίλυση της εξίσωσης του Laplace ξεκινά με έναν πίνακα δυο διαστάσεων πραγματικών αριθμών που αναπαριστούν την τάση των σημείων πλέγματος του αγώγιμου φύλλου. Για να πάρουμε μια περισσότερο ακριβή λύση, ο αριθμός των σημείων αυξάνεται όμως και ο αριθμός των υπολογισμών που απαιτούνται. Μετά την αρχικοποίηση του διδιάστατου πίνακα, η τεχνική του αλγορίθμου είναι εξαιρετικά απλή: ξανά-υπολογίζεται η τιμή κάθε σημείου του πίνακα χρησιμοποιώντας το μέσο όρο των τεσσάρων πιο κοντινών του σημείων. Αυτός ο επανυπολογισμός επαναλαμβάνεται για πολλές επαναλήψεις, μέχρι η λύση να προσεγγίσει κάποια επιθυμητή ακρίβεια.

Είναι φανερό ότι ο συγκεκριμένος αλγόριθμος μπορεί να υλοποιηθεί παράλληλα, γιατί η ενημέρωση της τιμής κάθε σημείου είναι εντελώς ανεξάρτητη και μπορεί να πραγματοποιηθεί παράλληλα με τον υπολογισμό άλλων σημείων. Η μόνη δυσκολία είναι το γεγονός ότι κάθε επανάληψη εξαρτάται από τις τιμές που έχουν υπολογιστεί στην προηγούμενη και συνεπώς οι επαναλήψεις δεν μπορούν να πραγματοποιηθούν παράλληλα. Ένας ακολουθιακός αλγόριθμος Jacobi δίνεται στο σχήμα 6.3. Το πρόγραμμα είναι ιδιαίτερα εύκολο. Ένας πίνακας A κρατά τις αρχικές τιμές όλων των σημείων. Ο βασικός επαναληπτικός βρόχος πραγματοποιεί numiter επαναλήψεις. Κατά τη διάρκεια κάθε επανάληψης, υπολογίζεται μια νέα τιμή για κάθε σημείο από το μέσο όρο των τεσσάρων γειτονικών του - το επάνω, κάτω, αριστερό και δεξί σημείο. Καθώς κάθε νέα τιμή υπολογίζεται αποθηκεύεται σε ένα προσωρινό πίνακα B για να αποφευχθεί η ανάμειξή του στους υπόλοιπους υπολογισμούς. Μετά τον υπολογισμό όλων των νέων τιμών ο προσωρινός πίνακας B γράφεται στον A πριν από την επόμενη επανάληψη. Το γεγονός ότι κάθε νέα τιμή υπολογίζεται χρησιμοποιώντας τις τρέχουσες τιμές αποτελεί σημαντική ιδιότητα του αλγορίθμου Jacobi. Οι νέες τιμές αντικαθιστούν τις παλιές μόνο μετά των υπολογισμό τους.

PROGRAM Jacobi;


CONST n = 32; (*Μέγεθος του πίνακα *)


      numiter = ...; (*Πλήθος των επαναλήψεων*)


VAR A, B: ARRAY [0..n+1,0..n+1] of Real;


    i, j, k: Integer;


BEGIN


    For i:= 0 to n+1 do (*Αρχικοποίηση των τιμών του πίνακα*)


    BEGIN


          For j:= 0 to n+1 do


                  Read(A[i, j]);


          Readln;


    END;


    B:= A;


    For k:= 1 to numiter do


        BEGIN


               For i:= 1 to n do


                        For j:= 1 to n do (*Υπολογισμός του μέσου όρου των τεσσάρων γειτονικών σημείων*)


                            B[i,j]=(A[i-1,j]+A[i+1,j]+A[i,j-1]+A[i,j+1]) / 4;


             A:= B;


        END;


END.

ΣΧΗΜΑ 6.3 Ακολουθιακό πρόγραμμα αλγορίθμου Jacobi

Μια ενδιαφέρουσα πλευρά αυτού του προγράμματος είναι η τεχνική που χρησιμοποιείται γαι να διατηρηθούν οι τιμές των ορίων σταθερές. Ο πίνακας A κρατά τις τιμές από 0 μέχρι n+1, αλλά το πρόγραμμα επαναλαμβάνει μόνο τις τιμές από το 0 ως το n. Με τον τρόπο αυτό οι τέσσερις οριακές τιμές του πίνακα μένουν αμετάβλητες. Εφόσον ο προσωρινός πίνακας B αντιγράφεται στον A μετά από κάθε επανάληψη, οι οριακές τιμές πρέπει να αρχικοποιηθούν στον πίνακα B. Αυτό γίνεται με την αντιγραφή όλου του πίνακα A στον πίνακα B κατά τη διάρκεια της αρχικοποίησης.