9.4 Αλγόριθμος JACOBI

Επόμενο:9.5 Περίληψη Πάνω: Κεφάλαιο 9o : Επιμερισμός δεδομένων Πίσω: 9.3 Πολλαπλασιασμός Μήτρας

9.4 Αλγόριθμος JACOBI

Ο παράλληλος αλγόριθμος Jacobi επιλύει μια σημαντική διαφορική εξίσωση που ονομάζεται εξίσωση του Laplace. Ο αλγόριθμος χρησιμοποιεί υπολογιστικές μεθόδους που είναι τυπικές για ένα μεγάλο εύρος αριθμητικών αλγορίθμων. Ο αλγόριθμος αρχίζει με αρχικές τιμές για ένα δι-διάστατο πίνακα. Αυτοί οι αριθμοί αντανακλούν κάποια φυσική ποσότητα στο φυσικό σύστημα που μοντελοποιείται, όπως είναι η τάση, η θερμοκρασία ή η πίεση. Ο αλγόριθμος επαναληπτικά υπολογίζει την τιμή σε κάθε σημείο του πίνακα ως το μέσο όρο των τεσσάρων γειτονικών σημείων. Ο όρος “χαλάρωση” χρησιμοποιείται γιατί οι τιμές σταδιακά εξισορροπούνται ή “χαλαρώνουν” σε όλον τον πίνακα. Τυπικά, τα οριακά σημεία διατηρούνται σε κάποια σταθερή καθορισμένη τιμή.

Στον αλγόριθμο Jacobi μέσα σε κάθε επανάληψη υπάρχει πολύ μεγάλη δυνατότητα παραλληλισμού. Στο κεφάλαιο 6 παρουσιάσαμε πολλές παράλληλες εκδόσεις για εκτέλεση σε συστήματα διαμοιραζόμενης μνήμης. Το τμήμα αυτό θα περιγράψει την εφαρμογή του παράλληλου αλγορίθμου Jacobi σε σύστημα κατανεμημένης μνήμης τοπολογίας Υπερκύβου. Θα επικεντρωθούμε στη μέθοδο επιμερισμού των δεδομένων και στα επαναληπτικά πρότυπα επικοινωνίας Υπερκύβου που προκύπτουν. Αναφορικά, το σχήμα 9.12 είναι το ακολουθιακό πρόγραμμα του αλγότιθμου Jacobi από το κεφάλαιο 6.

9.4.1 Αλγόριθμος συστήματος κατανεμημένης μνήμης.

Το κύριο θέμα στη δημιουργία ενός αλγορίθμου για σύστημα κατανεμημένης μνήμης είναι το πώς θα γίνει ο επιμερισμός των δεδομένων του πίνακα. Από τη στιγμή που θα αποφασιστεί η μέθοδος επιμερισμού ο αλγόριθμος ακολουθεί εύκολα. Στην έκδοση συστήματος διαμοιραζόμενης μνήμης στο κεφάλαιο 6 σε κάθε επεξεργαστής ανατίθεται μια μόνο γραμμή του πρωταρχικού πίνακα Α. Παρόλο που αυτός ο επιμερισμός με βάση τη γραμμή δεν είναι βέλτιστος οδηγεί στο πιο απλό πρόγραμμα και είναι επαρκές για τους σκοπούς μας. Για την εφαρμογή του αλγόριθμου Jacobi σε σύστημα κατανεμημένης μνήμης χρησιμοποιούμε την ίδια τεχνική επιμερισμού: σε κάθε επεξεργαστή θα ανατεθεί μια γραμμή του αρχικού πίνακα Α.

PROGRAM Jacobi;


CONST n=32;


        tolerance= 0.1;


VAR A, B: ARRAY [0..n+1,0..n+1] OF REAL;


    i,j : INTEGER;


    change,maxchange: REAL;


BEGIN


    .... (*Ανάγνωση των αρχικών τιμών για τον πίνακα Α*)


    B:= A;


    REPEAT (*Υπολογισμός των νέων τιμών μέχρι να επιτευχθεί η επιθυμητή ανοχή*)


    BEGIN


        maxchange:= 0;


        FOR i:= 1 TO n DO


            FOR j:=1 TO n DO


            BEGIN (*Υπολογισμός της νέας τιμής και της αλλαγής της σε σχέση με την παλιά τιμή*) 


                B[i,j]:= (A[i-1,j]+A[i+1,j]+A[i,j-1]+A[i,j+1])/4;


                change:= ABS(B[i,j]-A[i,j]);


                If change > maxchange THEN maxchange:= change;

            END;

    A:= B;

    END;

    UNTIL maxchange < tolerance;

END.

ΣΧΗΜΑ 9.12 Ακολουθιακός αλγόριθμος Jacobi με έλεγχο σύγκλισης

Η διαδικασία του υπολογισμού της νέας τιμής σε κάθε σημείο του πίνακα χρησιμοποιεί τις τιμές των τεσσάρων γειτονικών σημείων. Έτσι, κάθε σημείο χρειάζεται τιμές όχι μόνο από τη δική του γραμμή, αλλά και από τις επάνω και κάτω γειτονικές γραμμές. Στην έκδοση της διαμοιραζόμενης μνήμης του παράλληλου προγράμματος οι επεξεργαστές μπορούν να προσπελάσουν τις γειτονικές γραμμές εύκολα στην διαμοιραζόμενη μνήμη, η οποία περιέχει όλο τον πίνακα. Όμως, σε ένα σύστημα κατανεμημένης μνήμης δεν υπάρχει διαμοιραζόμενη μνήμη και οι γραμμές του πίνακα είναι κατανεμημένες στις τοπικές μνήμες των επεξεργαστών. Καθώς κάθε επεξεργαστής υπολογίζει τις νέες τιμές για τη δική του γραμμή, χρειάζεται κατά κάποιο τρόπο να έχει πρόσβαση και στις τιμές των δύο γειτονικών γραμμών. Σε αντιστοιχία με την τεχνική του περάσματος μηνυμάτων, οι τιμές που χρειάζονται θα σταλούν από τους γειτονικούς επεξεργαστές.

Υποθέστε ότι οι γραμμές κατανέμονται στους επεξεργαστές του συστήματος κατανεμημένης μνήμης, έτσι ώστε ο επεξεργαστής i να έχει την γραμμή i του πίνακα Α. Ο υπολογισμός που θα πραγματοποιηθεί στον επεξεργαστή i απαιτεί αντίγραφα των γραμμών i+1 και i-1 που βρίσκονται στους επεξεργαστές i+1 και i-1 αντίστοιχα. Κατά τη διάρκεια της φάσης επικοινωνίας του αλγορίθμου κάθε επεξεργαστής στέλνει ένα αντίγραφο της γραμμής του στους άμεσους γείτονες του. Έτσι κάθε επεξεργαστής θα έχει αντίγραφα από τρεις γραμμές: της δικής του γραμμής, της γραμμής που βρίσκεται πάνω από τη δική του και αυτής που βρίσκεται από κάτω. Χρησιμοποιώντας αυτές τις τρεις γραμμές κάθε επεξεργαστής έχει όλα τα δεδομένα που χρειάζεται για να υπολογίσει τις νέες τιμές για όλα τα στοιχεία της δικής του γραμμής, χρησιμοποιώντας την τεχνική μέσου όρου του Jacobi. Οι νέες τιμές για κάθε i γραμμή είναι διαθέσιμες μόνο στον επεξεργαστή i. Η επόμενη επανάληψη αρχίζει με κάθε επεξεργαστή να στέλνει πάλι ένα αντίγραφο αυτών των νέων τιμών και στους δύο άμεσους γείτονες του. Τότε κάθε επεξεργαστής μπορεί να λάβει τις νέες τιμές από τους δύο γείτονες του και να ξαναϋπολογίσει τη δική του γραμμή χρησιμοποιώντας τις νέες τιμές.

Ο αλγόριθμος συνεχίζει με τον ίδιο τρόπο, με κάθε επανάληψη να αποτελείται από μια φάση επικοινωνίας που ακολουθείται από μια φάση υπολογισμού. Η διαδικασία που ακολουθείται από κάθε επεξεργαστή είναι η ακόλουθη:

VAR myrow,downrow,uprow,newrow: ARRAY [0..n+1] OF REAL;


    j: INTEGER; done: BOOLEAN;


    maxchange: REAL;


BEGIN


REPEAT


    FOR j:= 1 TO n DO (*Μέσος όρος των τεσσάρων γειτονικών σημείων*)


        newrow[i]:= (myrow[j-1]+myrow[j+1]+downrow[j]+uprow[j])/4;


    myrow:= newrow;


    Send myrow to neighbors above nad below;


    Receive new copies of “downrow” and “uprow” from neighbors;

    Compute “maxchange” in my row;

    done:= Aggregate(maxchange < tolerance); (*Έλεγχος τερματισμού*)

UNTIL done;

END;

Στον παραπάνω υπολογισμό τα οριακά σημεία στις θέσεις 0 και i+1 του πίνακα διατηρούνται σταθερά. Γι’ αυτό το λόγο ο εσωτερικός βρόχος FOR λαμβάνει τιμές μόνο από το 1 ως το n. Παρατηρείστε ότι ο υπολογισμός μιας νέας τιμής σε κάθε σημείο απαιτεί δύο τιμές από την ίδια γραμμή, μια τιμή από την επάνω γραμμή και μια τιμή από τη γραμμή που βρίσκεται κάτω. Στο τέλος κάθε επανάληψης ο τοπικός έλεγχος τερματισμού γίνεται χρησιμοποιώντας τη συνάρτηση Aggregate για τον υπολογισμό του λογικού AND όλων των λογικών ελέγχων τερματισμού στις διεργασίες. Η συνάρτηση αυτή για τον Υπερκύβο έχει ήδη περιγραφεί με λεπτομέρειες στο κεφάλαιο 8.

Το πρότυπο αυτό της εναλλαγής του υπολογισμού με την επικοινωνία είναι όμοιο με τα προγράμματα των Ν-Σωμάτων και του Πολλαπλασιασμού Μήτρας που παρουσιάστηκαν προηγουμένως. Όμως, υπάρχει μια σημαντική διαφορά. Στα προγράμματα των Ν-Σωμάτων και του Πολλαπλασιασμού Μήτρας τα αντίγραφα των τμημάτων περιστρέφονται στις διεργασίες χωρίς καμία τροποποίηση-κάθε διεργασία λαμβάνει ένα αντίγραφο ενός τμήματος και μεταβιβάζει αυτό το ίδιο αντίγραφο. Όμως, στον αλγόριθμο Jacobi οι τιμές που κυκλοφορούν είναι συνέχεια νέες τιμές. Κάθε επεξεργαστής υπολογίζει νέες τιμές για τη δική του γραμμή και στη συνέχεια στέλνει αυτές τις νέες τιμές στους γείτονές του. Επειδή οι τιμές που κυκλοφορούν είναι συνεχώς νέες δεν είναι δυνατή η επικάλυψη της επικοινωνίας με τον υπολογισμό, όπως συμβαίνει στα προγράμματα των Ν-Σωμάτων και του Πολλαπλασιασμού Μήτρας. Θυμηθείτε ότι αυτή η επικάλυψη πραγματοποιείται κατά τη διάρκεια κάθε επανάληψης χρησιμοποιώντας την παρακάτω ακολουθία λειτουργιών: αποστολή, υπολογισμός, λήψη. Στον αλγόριθμο Jacobi πρέπει πρώτα να λάβουμε τις νέες τιμές και πριν τη φάση υπολογισμού, έτσι η ακολουθία των λειτουργιών να είναι η ακόλουθη: αποστολή, λήψη, υπολογισμός. Το ότι δεν είναι δυνατόν να επικαλυφθεί η επικοινωνία με τον υπολογισμό στον αλγόριθμο Jacobi αυξάνει την επίδραση των καθυστερήσεων επικοινωνίας στην απόδοση του αλγορίθμου σε σχέση με τα προγράμματα των Ν-Σωμάτων και του Πολλαπλασιασμού Μήτρας.

Το πλήρες παράλληλο πρόγραμμα του αλγόριθμου Jacobi για τον Υπερκύβο φαίνεται στο σχήμα 9.13. Η τοπολογία του Υπερκύβου έχει διάσταση 5 και συνεπώς περιέχει τους απαραίτητους 32 επεξεργαστές για τον πίνακα Α ο οποίος έχει 32 γραμμές.


PROGRAM Jacobi;


ARCHITECTURE HYPERCUBE(5);


CONST n=32; (*Αριθμός των επεξεργαστών*)


    d=5; (*Διάσταση του Υπερκύβου*)


    numiter=2*d; (*Πλήθος των επαναλήψεων πριν τον έλεγχο τερματισμού*)


    tolerance=.1;


TYPE rowtype= ARRAY [0..n+1] OF REAL;


VAR A: ARRAY [0..n+1] OF rowtype;


    i: INTEGER;


    upchan,downchan: ARRAY [1..n] OF CHANNEL OF rowtype; (*Θύρες επικοινωνίας*)


    GrayCode: ARRAY [1..n] OF INTEGER;


    inchan: ARRAY [0..n-1,1..d] OF CHANNEL OF BOOLEAN; (*Για την Συλλογή*)

 

FUNCTION Aggregate(mydone: BOOLEAN): BOOLEAN;


....(*Συνάρτηση Πολλαπλής Συλλογής από το σχήμα 8.11*)

 

PROCEDURE Updaterow(me: INTEGER; myrow: rowtype; VAR out: rowtype);


VAR j,k: INTEGER; maxchange,change: REAL;


    newrow,uprow,downrow: rowtype;


    done: BOOLEAN;


BEGIN


    newrow[0]:= myrow[0]; newrow[n+1]:= myrow[n+1];


    IF me= 1 THEN downrow:= downchan[me];


    IF me= n THEN uprow:= upchan[me];


    REPEAT


        FOR k:= 1 TO numiter DO (*Αρκετές επαναλήψεις πριν τον έλεγχο τερματισμού*)


        BEGIN


            IF me > 1 THEN

                upchan[me-1]:= myrow; (*Αποστολή στον γείτονα me-1*)

            IF me < n THEN 

            BEGIN

                downchan[me+1]:= myrow; (*Αποστολή στον γείτονα me+1*)

                uprow:= upchan[me]; (*Λήψης της νέας uprow*)

            END;

            IF me > 1 THEN 

                downrow:= downchan[me]; (*Λήψη της νέας downrow*)

            maxchange:= 0;

            FOR j:= 1 TO n DO

            BEGIN

            (*Υπολογισμός του μέσου όρου των γειτονικών σημείων*)

                newrow[j]:= (myrow[j-1]+myrow[j+1]+downrow[j]+uprow[j])/4;

                change:= ABS(newrow[j]-myrow[j]);

                IF change > maxchange THEN maxchange:= change;

            END;

            myrow:=newrow;

        END;

        done:= Aggregate(maxchange < tolerance); (*Έλεγχος τερματισμού*)

UNTIL done;

out:= myrow; (*Εγγραφή των τελικών αποτελεσμάτων στο F*)

END;

 

BEGIN

    ... (*Αρχικοποίηση των τιμών για τον πίνακα Α*)

    (*Αρχικοποίηση του πίνακα GrayCode για τον Υπερκύβο*)

 

    downchan[1]:= A[0]; upchan[n]:= A[n+1]; (*Καθορισμένες οριακές τιμές

    FORALL i:= 1 TO n DO 

        (@GrayCode[i] PORT upchan[i]; downchan[i]; inchan[GrayCode[i]])

    Updaterow(i, A[i], A[i]);

END.

ΣΧΗΜΑ 9.13 Αλγόριθμος Jacobi σε Υπερκύβο

Η επικοινωνία μεταξύ των διεργασιών γίνεται με τους πίνακες upchan και downchan, που επιτρέπουν την επικοινωνία όλης της γραμμής με μια μόνο έκφραση. Κάθε διεργασία έχει τις θύρες επικοινωνίας upchan[me] και downchan[me] για τη λήψη των γραμμών δεδομένων από τις γειτονικές διεργασίες. Για την ελαχιστοποίηση της καθυστέρησης επικοινωνίας οι διεργασίες που εργάζονται σε γειτονικές γραμμές πρέπει να εκτελούνται σε φυσικούς επεξεργαστές με απευθείας σύνδεση στην τοπολογία του Υπερκύβου. Για το σκοπό αυτό ένας Κώδικας Gray διατηρείται στον πίνακα GrayCode και κάθε i διεργασία ανατίθεται στον φυσικό επεξεργαστή με τον αριθμό GrayCode[i]. Για την μείωση της επιβάρυνσης της απόδοσης που αφορά τον έλεγχο τερματισμού, πραγματοποιούνται αρκετές επαναλήψεις μεταξύ των ελέγχων τερματισμού. Κάθε διεργασία στο πρόγραμμα δημιουργείται με τη διαδικασία Updaterow, που έχει τρεις παραμέτρους:

me ο αριθμός γραμμής στον πίνακα Α που έχει ανατεθεί στην συγκεκριμένη διεργασία

myrow αντίγραφο της γραμμής που έχει ανατεθεί από τον πίνακα Α

out για την επιστροφή των τελικών τιμών της γραμμής που έχει ανατεθεί πίσω στην κύρια

Η διαδικασία Update είναι η ίδια με αυτή που παρουσιάστηκε στον άτυπο αλγόριθμο πιο πριν, με τη διαφορά ότι τώρα έχουν προστεθεί λεπτομερείς εντολές για επικοινωνία. Κάθε διεργασία στέλνει ένα αντίγραφο της δικής της γραμμής myrow στο κατάλληλο κανάλι λήψης των δύο γειτονικών της διεργασιών. Η χρήση των upchan και downchan είναι η ακόλουθη: η downchan λαμβάνει τη γραμμή από τη γειτονική με τον μικρότερο αριθμό γραμμής και η upchan λαμβάνει από τη γειτονική με τον υψηλότερο αριθμό γραμμής. Οι έλεγχοι me1 και me n είναι απαραίτητοι για τις περιπτώσεις των οριακών σημείων. Οι διεργασίες στα ακραία άνω και κάτω όρια έχουν μόνο ένα γείτονα και συνεπώς πρέπει να επικοινωνούν μόνο προς μια κατεύθυνση.

Η δήλωση δημιουργίας διεργασίας στο σώμα του κυρίως προγράμματος είναι ίδια με τα προηγούμενα παραδείγματα προγραμμάτων. Κάθε διεργασία ανατίθεται στο φυσικό της επεξεργαστή χρησιμοποιώντας τον τελεστή @ με τον αριθμό του Κώδικα Gray. Η διεργασία i ανατίθεται στις θύρες επικοινωνίας upchan[i] και downchan[i]. Επίσης η διεργασία i πρέπει να ανατεθεί σε μια inchan θύρα για τη χρησιμοποίηση από τη συνάρτηση Aggregate κατά τη διάρκεια του ελέγχου τερματισμού. Έτσι, πρέπει να χρησιμοποιηθεί ένας διαφορετικός τρόπος αρίθμησης για αυτές τις inchan θύρες γιατί η συνάρτηση Aggregate αναφέρεται σε αριθμούς φυσικού επεξεργαστή όταν στέλνει μηνύματα (δες την ανάλυση για την Πολλαπλή Συλλογή σε Υπερκύβο στο τέλος του κεφαλαίου 8). Η διεργασία i ανατίθεται στο inchan[GrayCode[i]] γιατί ο GrayCode[i] είναι ο αριθμός φυσικού επεξεργαστή στον οποίο εκτελείται η διεργασία i.

9.4.2 Ανάλυση απόδοσης

Ο αριθμός των επαναλήψεων που απαιτούνται για τη σύγκλιση στο πρόγραμμα του αλγόριθμου Jacobi εξαρτάται από τις ιδιότητες των τιμών των αρχικών δεδομένων. Στην ανάλυση απόδοσης το θέμα αυτό μπορεί να παρατηρηθεί αν επικεντρωθούμε στο μέσο χρόνο εκτέλεσης για κάθε επανάληψη. Η ανάλυση είναι παρόμοια με αυτή του προγράμματος των Ν-Σωμάτων και του Πολλαπλασιασμού Μήτρας. Τα σύμβολα που θα χρησιμοποιήσουμε είναι τα ακόλουθα:

n αριθμός των γραμμών στον πίνακα Α (και αριθμός επεξεργαστών)

d διάσταση του Υπερκύβου

D καθυστέρηση επικοινωνίας του κοντινότερου επεξεργαστή στον Υπερκύβο

Όπως και προηγουμένως, κάθε επανάληψη έχει μια φάση υπολογισμού και μια φάση επικοινωνίας. Η φάση υπολογισμού σε κάθε διεργασία υπολογίζει τις νέες τιμές για τα n σημεία της γραμμής που έχει ανατεθεί στην συγκεκριμένη διεργασία. Αυτό γίνεται στην διαδικασία Update με έναν FOR βρόχο του οποίου ο δείκτης j λαμβάνει τιμές από το 1 ως το n. Η διάρκεια αυτής της φάσης έχει τη γενική μορφή:

Φάση υπολογισμού: Sn

Κατά τη διάρκεια της φάσης υπολογισμού n τιμές στέλνονται σε καθέναν από τους δύο επεξεργαστές. Όπως αναλύσαμε και σε προηγούμενες παραγράφους, ο συνολικός αριθμός των πακέτων που στέλνονται σε κάθε γείτονα είναι n/3 και συνεπώς η καθυστέρηση στο δίκτυο επικοινωνίας είναι:

Επιπλέον, υπάρχει κάποια επιβάρυνση λογισμικού για την εκτέλεση των δηλώσεων επικοινωνίας στην αρχή κάθε επανάληψης στη διαδικασία Update. Αυτή η επιβάρυνση αυξάνεται ανάλογα με το n, αλλά στην ουσία κυριαρχείται από μια σταθερά χρόνου που είναι ανεξάρτητη από το n. Αυτό μπορεί να προστεθεί στον παραπάνω χρόνο καθυστέρησης υλικού για να λάβουμε την ακόλουθη γενική μορφή για τη διάρκεια της φάσης επικοινωνίας:

Φάση επικοινωνίας:

Εφόσον δεν υπάρχει επικάλυψη μεταξύ του υπολογισμού και της επικοινωνίας, η διάρκεια των δύο φάσεων απλά προστίθεται για να πάρουμε τη διάρκεια μιας επανάληψης:

Επανάληψη:

Αναφορικά με το πρόγραμμα Jacobi του σχήματος 9.13 είδαμε ότι μετά από κάθε 2d επαναλήψεις πραγματοποιείται έλεγχος τερματισμού με την κλήση της συνάρτησης Aggregate. Έτσι, ο χρόνος εκτέλεσης της συνάρτησης Aggregate πρέπει να είναι ο μέσος όρος σε αυτές τις 2d επαναλήψεις. Στο κεφάλαιο 8 είδαμε ότι η συνάρτηση Aggregate έχει logn=4 επαναλήψεις με μια μικρή φάση υπολογισμού και επικοινωνίας. Ο υπολογισμός αποτελείται από μερικές δηλώσεις ανάθεσης και η επικοινωνία αφορά την αποστολή και τη λήψη μιας μόνο τιμής από έναν άμεσο γείτονα. Το άθροισμα αυτών των χρόνων θα είναι μια σταθερά, η οποία πρέπει να πολλαπλασιαστεί με τον αριθμό των επαναλήψεων για να καθοριστεί η διάρκεια της συνάρτησης Aggregate:

Συνάρτηση Aggregate: dG

Εφόσον η συνάρτηση Aggregate καλείται μετά από κάθε 2d επαναλήψεις Jacobi στην διαδικασία Update, ο χρόνος εκτέλεσής της πρέπει να διαιρεθεί με 2d και να προστεθεί στο χρόνο για την επανάληψη Jacobi:

Και συνδυάζοντας τις σταθερές μπορεί να γραφεί:

Μέση επανάληψη Jacobi:

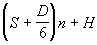
Σε αυτή την ανάλυση επιλέξαμε να αγνοήσουμε τη δημιουργία διεργασιών και τη φάση αρχικοποίησης των δεδομένων. Ειδικά, είναι ενδιαφέρουσα η εξέταση της μεταβολής της απόδοσης του προγράμματος καθώς αυξάνεται το n. Η τιμή του n αναφέρεται στο μέγεθος του πίνακα δεδομένων και επίσης στον αριθμό των επεξεργαστών. Συνεπώς, είναι μια σημαντική παράμετρος. Μια χρήσιμη μέτρηση της απόδοσης του προγράμματος για τις ποικίλες τιμές του n είναι η απόδοση, που καθορίζεται ως η επιτάχυνση δια τον αριθμό των επεξεργαστών.

Η επιτάχυνση ορίζεται σαν ο ακολουθιακός χρόνος εκτέλεσης δια τον παράλληλο χρόνο εκτέλεσης. Ένας λογικός ορισμός του ακολουθιακού χρόνου εκτέλεσης σε αυτό το πρόγραμμα Jacobi είναι ο χρόνος που απαιτείται για την φάση υπολογισμού κάθε επανάληψης χρησιμοποιώντας μόνο έναν επεξεργαστή. Ο χρόνος επικοινωνίας και ο χρόνος για την εκτέλεση της συνάρτησης Aggregate θεωρούνται ως επιβαρύνσεις που έχουν σχέση με την παράλληλη εκτέλεση και συνεπώς δεν συμπεριλαμβάνονται στον ακολουθιακό χρόνο. Εφόσον καθεμία από τις n διεργασίες απαιτεί Sn χρόνο για την φάση υπολογισμού κάθε επανάληψης ο ακολουθιακός χρόνος εκτέλεσης για κάθε επανάληψη είναι:

Ακολουθιακός χρόνος: Sn²

Για να ορίσουμε την επιτάχυνση που επιτυγχάνεται από το παράλληλο πρόγραμμα διαιρούμε αυτόν τον ακολουθιακό χρόνο με τον μέσο παράλληλο χρόνο για κάθε επανάληψη Jacobi:

Επιτάχυνση:

Καθώς αυξάνεται το n η επιτάχυνση θα προσεγγίσει το όριο

Μέγιστη επιτάχυνση:

Το σχήμα 9.14 δείχνει ένα γράφημα της πραγματικής απόδοσης του προγράμματος Jacobi για διάφορες τιμές του n. Ο κάθετος άξονας δείχνει την απόδοση, που καθορίζεται ως η επιτάχυνση δια n, που είναι ο αριθμός των επεξεργαστών. Η μέγιστη απόδοση που μπορεί να επιτευχθεί σε κάθε παράλληλο πρόγραμμα είναι, φυσικά, 1. Καθεμία από τις τέσσερις καμπύλες στο σχήμα δείχνει την απόδοση που επιτυγχάνεται καθώς το n ποικίλει για μια δεδομένη καθορισμένη τιμή της βασικής καθυστέρησης επικοινωνίας D. Οι τέσσερις τιμές δείγματος του D είναι 0, 20, 40, 60. Αυτές οι τέσσερις καμπύλες βασίζονται σε μετρήσεις του μέσου χρόνου εκτέλεσης κάθε επανάληψης. Όπως και παραπάνω στην ανάλυση απόδοσης, έτσι και σε αυτές τις μετρήσεις η δημιουργία της διεργασίας και οι τιμές αρχικοποίησης των δεδομένων δεν συμπεριλαμβάνονται. Η ανάλυση απόδοσης προβλέπει ότι η απόδοση θα πρέπει να προσεγγίσει το ακόλουθο όριο καθώς αυξάνεται το n:

Μέγιστη αποδοτικότητα:

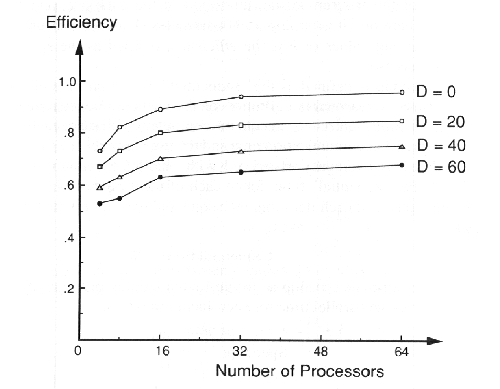
ΣΧΗΜΑ 9.14 Απόδοση του αλγόριθμου Jacobi

Στο σχήμα αυτό βλέπουμε ότι κάθε καμπύλη φαίνεται να προσεγγίζει κάποια οριακή τιμή, σύμφωνα και με την παραπάνω πρόβλεψη της απόδοσης. Ο παραπάνω τύπος προβλέπει ότι η απόδοση για D=1 θα προσεγγίσει την οριακή τιμή 1. Η καμπύλη που παρατηρήθηκε για D=0 φαίνεται ότι ακολουθεί αυτή την γενική ιδιότητα. Φαίνεται επίσης στο σχήμα 9.14 ότι η αύξηση της βασικής καθυστέρησης επικοινωνίας D για να παραχθούν οι άλλες καμπύλες μειώνει σταδιακά την αποδοτικότητα, που συμφωνεί και με την παραπάνω θεωρητική πρόβλεψη. Ο υπολογισμός των καμπύλων απόδοσης έγινε με την Multi-Pascal και τη βοήθεια των παρακάτω στοιχείων: Duration, %Seqon, Seqtime, Clock (Δες το Παράρτημα για την περιγραφή της χρήσης αυτών των στοιχείων για τις μετρήσεις απόδοσης).

9.4.3 Εναλλακτικές Μέθοδοι Επιμερισμού

Το πρόγραμμα του Παράλληλου Αλγορίθμου Jacobi του σχήματος 9.13 επιμερίζει τον πίνακα Α κατά γραμμές, με ακριβώς μια γραμμή για κάθε επεξεργαστή. Σε μια πραγματική εφαρμογή ο αριθμός των γραμμών στον πίνακα μπορεί να είναι μεγαλύτερος από τον αριθμό των διαθέσιμων επεξεργαστών. Σε αυτή την περίπτωση μπορεί να χρησιμοποιηθεί μια παρόμοια τεχνική επιμερισμού γραμμής, όπου σε κάθε επεξεργαστή ανατίθεται μια ομάδα γραμμών. Αν έχουμε n γραμμές και p επεξεργαστές, τότε σε κάθε επεξεργαστή ανατίθενται n/p γραμμές. Σε αυτό τον επιμερισμό δεν χρειάζεται να επικοινωνούν όλες οι γραμμές των επεξεργαστών με τις γειτονικές τους κατά τη διάρκεια κάθε επανάληψης-μόνο οι οριακές γραμμές χρειάζεται να επικοινωνούν.

Ο λόγος για αυτή την επικοινωνία είναι να παρέχει σε κάθε σημείο όλες τις γειτονικές του τιμές για την έναρξη κάθε επανάληψης. Όταν κάθε επεξεργαστής έχει ένα τμήμα που αποτελείται μόνο από μια γραμμή, τότε αυτή η γραμμή είναι επίσης οριακή και πρέπει να σταλεί σε κάθε γείτονα. Όμως, αν υπάρχουν πολλές γραμμές σε ένα τμήμα, μόνο η πρώτη και η τελευταία γραμμή κάθε τμήματος πρέπει να μπουν σε διαδικασία επικοινωνίας. Οι εσωτερικές γραμμές κάθε τμήματος δεν επηρεάζουν άμεσα γραμμές σε άλλα τμήματα. Με αυτό τον επιμερισμό πολλαπλών γραμμών, η ποσότητα της επικοινωνίας των δεδομένων από κάθε διεργασία κατά τη διάρκεια κάθε επανάληψης είναι 2n.

Για να μειώσουμε την ποσότητα της επικοινωνίας είναι περισσότερο αποδοτικό αν επιμερίσουμε τον πίνακα κατά έναν δι-διάστατο τρόπο, όπως κάναμε και με τους πίνακες στο πρόγραμμα του Πολλαπλασιασμού Μήτρας. Αυτός ο επιμερισμός σε ένα δι-διάστατο πίνακα τετράγωνων τμημάτων ελαχιστοποιεί τον αριθμό των οριακών σημείων σε κάθε τμήμα. Ο αριθμός των οριακών σημείων για αυτές τις διαφορετικές επιμεριστικές μεθόδους φαίνεται στο σχήμα 9.15. Στο πάνω τμήμα του σχήματος ο nxn πίνακας επιμερίζεται κατά γραμμές σε p τμήματα. Ο αριθμός των οριακών σημείων είναι πάντα 2n και είναι ανεξάρτητος του p. Με δι-διάστατο επιμερισμό καθένα από τα p τμήματα είναι ένα τετράγωνο με n²/p σημεία. Το τμήμα περιέχει γραμμές και στήλες. Ο συνολικός αριθμός των οριακών σημείων σε αυτή την περίπτωση είναι .

Για μεγάλους πίνακες ο δι-διάστατος επιμερισμός έχει λιγότερα οριακά σημεία. Για παράδειγμα, θεωρείστε έναν 128x128 πίνακα και τη χρήση ενός συστήματος κατανεμημένης μνήμης με 64 επεξεργαστές. Χρησιμοποιώντας την τεχνική επιμερισμού γραμμής, κάθε τμήμα θα έχει 2n=256 οριακά σημεία. Με τον δι-διάστατο επιμερισμό, θα έχουμε έναν πίνακα 8x8 με τετράγωνα τμήματα καθένα από τα οποία θα έχει διάσταση 16x16. Συνεπώς, ο αριθμός των οριακών σημείων είναι 64, που είναι το 1/4 σε σχέση με την μέθοδο του επιμερισμού γραμμής. Ένα μειονέκτημα του δι-διάστατου επιμερισμού είναι ότι οδηγεί σε ένα πιο πολύπλοκο πρόγραμμα, γιατί κάθε επεξεργαστής πρέπει να επικοινωνεί απευθείας με τέσσερις γείτονες, ενώ στη μέθοδο επιμερισμού γραμμής κάθε επεξεργαστής πρέπει να επικοινωνεί μόνο με δυο γείτονες.

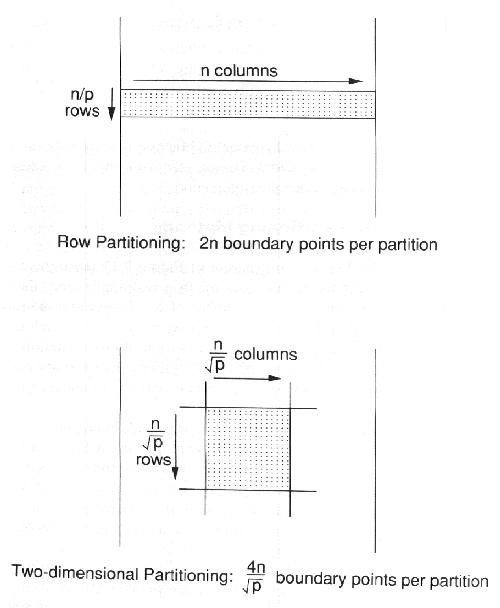
ΣΧΗΜΑ 9.15 Οριακά σημεία για τους διαμερισμούς

Επόμενο:9.5 Περίληψη Πάνω: Κεφάλαιο 9o : Επιμερισμός δεδομένων Πίσω: 9.3 Πολλαπλασιασμός Μήτρας