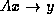 , x and y distributed like vectors:
For this case,
assume that x and y are identically distributed according to
the inducing vector distribution that induced the distribution of matrix A .
Notice that by spreading vector x within columns, we duplicate
all necessary elements of x so that local matrix vector multiplication
can commence on each node. After this, a reduction (summation) within rows of nodes
of the local partial results yields the desired vector y .
However, since only a portion of vector y needs to be known to
each node, a
distributed reduction (MPI_Reduce_scatter)
within rows of nodes suffices. This process is illustrated
in Figure 1.5.
In this figure, the matrix
, x and y distributed like vectors:
For this case,
assume that x and y are identically distributed according to
the inducing vector distribution that induced the distribution of matrix A .
Notice that by spreading vector x within columns, we duplicate
all necessary elements of x so that local matrix vector multiplication
can commence on each node. After this, a reduction (summation) within rows of nodes
of the local partial results yields the desired vector y .
However, since only a portion of vector y needs to be known to
each node, a
distributed reduction (MPI_Reduce_scatter)
within rows of nodes suffices. This process is illustrated
in Figure 1.5.
In this figure, the matrix 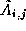 denotes the sub-matrix
of A assigned to node (i,j) .
denotes the sub-matrix
of A assigned to node (i,j) .
In general,
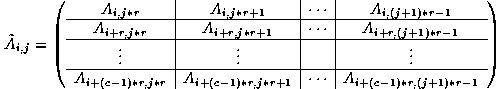
After spreading the sub-vectors of x within
columns of nodes, node (i,j) holds the following sub-vectors:

Thus, all sub-vectors of x required for the
local matrix-vector multiply are in place.
After executing the local matrix-vector multiply,
each node owns a local contribution to part of y ,
so that
a summation of the results within rows of nodes
completes the matrix-vector multiply,
leaving the appropriate piece of
the result vector on each node,
We will see that this summation within one dimension of the mesh
becomes a basic operation in PLAPACK, in Chapter  .
.
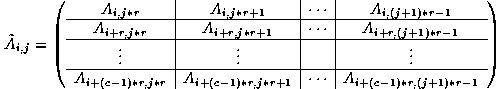

![]() .
.