For this operation to be well-defined, we require
matrices A , B , and C to have dimensions ![]() ,
,
![]() , and
, and ![]() , respectively.
, respectively.
We start my noting that if we partition A and B by columns and rows, respectively,
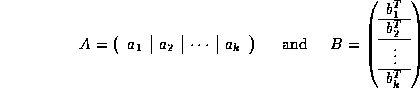
then
![]()
Thus, a matrix-matrix multiply can be written as a sequence of rank-one updates.
We can implement the above sequence of rank-1 updates by using views, splitting off one column and row at a time: Let A and B be partitioned like
![]()
where ![]() and
and ![]() equal the first column of A and
first row of B .
Then
equal the first column of A and
first row of B .
Then
![]()
So the update of C can be viewed as an initial
scaling of C , followed by a rank-1 update with the
first column and row of A and B, respectively.
After this, the operation ![]() can
be performed, using the same approach, recursively.
can
be performed, using the same approach, recursively.
This leads to the following algorithm:
Here the ``
- Scale
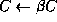
- Let
and
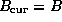
- Do until done
- If
and
are empty, the loop is done.
- Partition
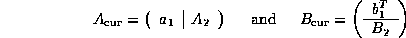
- Update
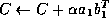
- Let
and
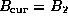
PLACE BEGIN HR HERE

PLACE END HR HERE
In order to get better performance,
it is advantageous to set up the algorithm
to perform a sequence of rank-k![]() updates instead:
Let A and B be partitioned like
updates instead:
Let A and B be partitioned like
![]()
where ![]() and
and ![]() are is a
are is a ![]() and
and ![]() matrices, respectively.
Then
matrices, respectively.
Then
![]()
This leads to the following algorithm:
Again, the ``
- Scale
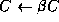
- Let
and
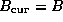
- Do until done
- Determine width s of split. If
and
are empty, the loop is done.
- Partition

and

where
and
are is a
and
matrices, respectively.
- Update
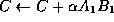
- Let
and
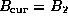
PLACE BEGIN HR HERE

PLACE END HR HERE
When k is large, the above algorithm can be improved by introducing pipelining. This can be accomplished by setting the natural flow of computation to be to the right for communication within rows and down for communication within columns. We will assume this has been done before entering the matrix multiplication routine, using the calls
For details on the benefits of pipelining, see [, ].PLA_Temp_set_comm_dir( template, PLA_TEMP_ROW, PLA_DIR_RIGHT ); PLA_Temp_set_comm_dir( template, PLA_TEMP_COL, PLA_DIR_DOWN );