Let us further consider the matrix-matrix multiply.
We claim
for each of the
four cases given in Equations ![]() -
-![]() ,
there are actually eight different cases to
be considered. The different cases correspond to
the cases where each of the matrix dimensions m , n , and
k are either large or small. Since there are three
dimensions and two possibilities for each dimension, there
are
,
there are actually eight different cases to
be considered. The different cases correspond to
the cases where each of the matrix dimensions m , n , and
k are either large or small. Since there are three
dimensions and two possibilities for each dimension, there
are ![]() cases. These different cases are tabulated
in Tables
cases. These different cases are tabulated
in Tables ![]() and
and ![]() .
In these tables, the diagrams indicating matrix shapes illustrate
the layout of data in its non-transposed format.
Transposition is indicated by the superscript ``
.
In these tables, the diagrams indicating matrix shapes illustrate
the layout of data in its non-transposed format.
Transposition is indicated by the superscript `` ![]() ''.
We will discuss general approaches to each of the different
cases in the rest of this section.
''.
We will discuss general approaches to each of the different
cases in the rest of this section.
Let us reconsider the formation of ![]() .
Notice that if we partition a given matrix X
by columns and by rows:
.
Notice that if we partition a given matrix X
by columns and by rows:
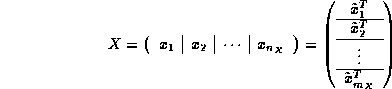
where ![]() , then C can be computed
by any of the following formulae:
, then C can be computed
by any of the following formulae:
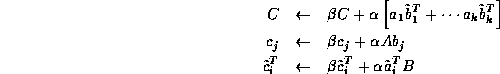
which suggests besides the panel-panel variant for forming C ,
there are also matrix-panel and panel-matrix variants.
Similarly, there are panel-panel, matrix-panel, and panel-matrix
variants for each of the three other matrix-matrix multiplies
in Equations ![]() -
-![]() .
.
The choice of variants presented in previous subsections
are optimal for this case.
The primary issue is that good load balance can be
obtained, since all nodes have a reasonable portion
of the individual panel-panel, matrix-panel or panel-matrix
operation to perform.
A secondary issue is that except
for the case ![]() ,
all communication can be performed using only
broadcasts and reduction-to-one within one or the other
dimension of the mesh of nodes. Thus, no packing
needs to be performed in the copy and/or reduce.
In other words, the individual panels need not be transposed
as described in Section 1.4.2.
,
all communication can be performed using only
broadcasts and reduction-to-one within one or the other
dimension of the mesh of nodes. Thus, no packing
needs to be performed in the copy and/or reduce.
In other words, the individual panels need not be transposed
as described in Section 1.4.2.
Notice that in the tables, it is indicated that this
defaults to a rank-1 update when k = 1 . From this,
we deduce that if k is small, a panel-panel
variant is the appropriate choice,
since in the limit it becomes a rank-1 update.
Notice that for the cases where A is transposed
(e.g. ![]() and
and ![]() ),
this means that the contributions from A
present themselves as row panels, which must be
spread within rows, requiring a transpose of each panel,
as described in Section 1.4.2.
Similarly,
for the cases where B is transposed
(e.g.
),
this means that the contributions from A
present themselves as row panels, which must be
spread within rows, requiring a transpose of each panel,
as described in Section 1.4.2.
Similarly,
for the cases where B is transposed
(e.g. ![]() and
and ![]() ),
the contributions from B
present themselves as column panels, which must be
spread within columns, also requiring a transpose of each panel,
as described in Section 1.4.2.
),
the contributions from B
present themselves as column panels, which must be
spread within columns, also requiring a transpose of each panel,
as described in Section 1.4.2.
Notice that in the tables, it is indicated that this defaults to a matrix-vector multiply when n = 1 . From this, we deduce that if n is small, a matrix-panel variant is the appropriate choice, since it defaults to a matrix-vector multiply when n = 1 . For similar reasons as for the last case, depending of whether A and B are to be transposed, the views of matrices C and B change, and the reduction and spreading may require a transpose operation for each panel of C and/or B .
In the tables, it is indicated that this defaults to an axpy-like operation when n = 1 and k = 1 . From this, we deduce that if n and k are small, this operation will be at least as efficient as the appropriate case of the axpy operation. One can envision an efficient implementation that redistributes panels of rows and/or columns as multivectors and performs axpy-like operations using all nodes.
This case is similar to the one where m is large, and n is small. This time, a panel-matrix variant appears appropriate.
This case is similar to the one where m is large, and n is small, suggesting an axpy-like approach.
This defaults to an inner product-like operation when m = 1 and n = 1 . One approach could be to redistribute panels of rows and/or columns as multivectors, and performing inner product-like operations using all nodes.
This operation becomes the totally degenerate case of a simple scalar multiplication when m = n = k = 1 , n = 1 . From this, we deduce that if m , n , and k are small, one should consider performing it on a single processor, i.e., redistributing the matrices as multiscalars.
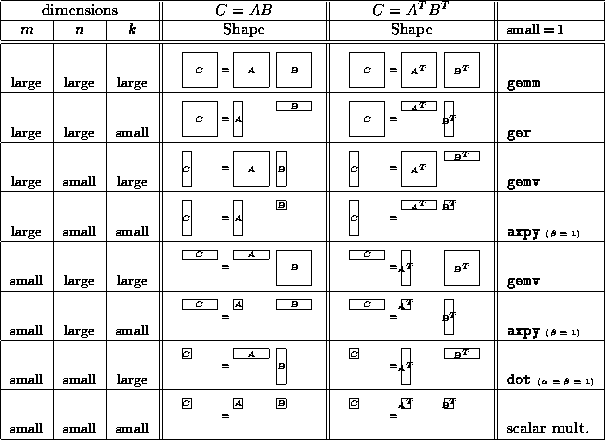
Table: Different possible cases for matrix-matrix multiply, Part I.
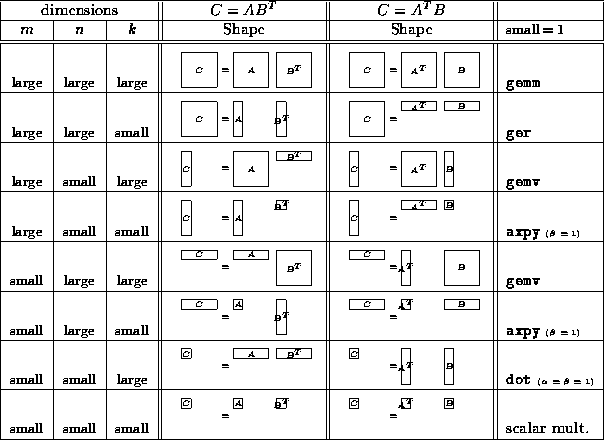
Table: Different possible cases for matrix-matrix multiply, Part II.