In order to take advantage of the higher performance of sequential level-3 BLAS, we rewrite the above algorithm in terms of matrix-matrix operations. Partition
![]()
where ![]() and
and ![]() are
are ![]() sub-matrices.
Now,
sub-matrices.
Now,
![]()
This in turn yields the equations

We thus conclude that the following steps will implement the Cholesky factorization, overwriting the lower triangular portion of A with L :
Notice that to compute
, where Cholesky factor
overwrites the lower triangular part of
.
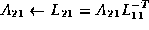
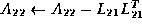
- compute the Cholesky factorization of updated
recursively, yielding
.
The PLAPACK code for this level-3 BLAS based implementation is given
in
Figure 8.2.
Notice that the block size b must be determined. This block size
should equal the width of ![]() that makes the
the symmetric rank-k update:
that makes the
the symmetric rank-k update: ![]() most efficient.
The call
most efficient.
The call
PLA_Environ_nb_alg( PLA_OP_SYM_PAN_PAN, template, &nb_alg );queries the infrastructure for the optimal block size for symmetric rank-k (panel-panel) update. A second optimization, which could also have been used for the level-2 BLAS right-looking variant, recognizes that computation naturally flows to the right and down: notice that the columns are completed from left to right, and similarly the order in which rows no longer participate is from top to bottom. The calls
PLA_Temp_get_comm_dir( template, PLA_DIR_TEMP_ROW, &old_dir_row );query the current directions of the flow of computation, sets them as appropriate for the Cholesky factorization, and resets them after the Cholesky factorization has completed.
PLA_Temp_get_comm_dir( template, PLA_DIR_TEMP_COL, &old_dir_col );
PLA_Temp_set_comm_dir( template, PLA_DIR_TEMP_ROW, PLA_DIR_RIGHT );
PLA_Temp_set_comm_dir( template, PLA_DIR_TEMP_COL, PLA_DIR_DOWN );
PLA_Temp_set_comm_dir( template, PLA_DIR_TEMP_ROW, old_dir_row );
PLA_Temp_set_comm_dir( template, PLA_DIR_TEMP_COL, old_dir_col );